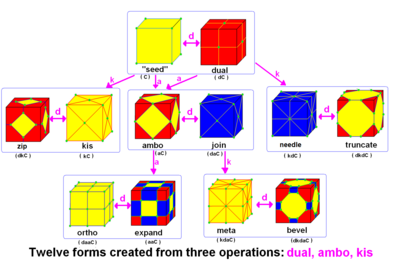

In geometry, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.
Conway and Hart extended the idea of using operators, like truncation defined by Kepler, to build related polyhedra of the same symmetry. The basic descriptive operators can generate all the Archimedean solids and Catalan solids from regular seeds. For example, tC represents a truncated cube, and taC, parsed as t(aC), is a truncated cuboctahedron. The simplest operator dual swaps vertex and face elements, like a dual cube is an octahedron: dC=O. Applied in a series, these operators allow many higher order polyhedra to be generated. A resulting polyhedron will have a fixed topology (vertices, edges, faces), while exact geometry is not constrained: it can be thought of as one of many embeddings of a polyhedral graph on the sphere.
The seed polyhedra are the Platonic solids, represented by the first letter of their name (T,O,C,I,D); the prisms (Pn) for n-gonal forms, antiprisms (An), cupolae (Un), anticupolae (Vn) and pyramids (Yn). Any polyhedron can serve as a seed, as long as the operations can be executed on it. For example regular-faced Johnson solids can be referenced as Jn, for n=1..92.
In general, it is difficult to predict the resulting appearance of the composite of two or more operations from a given seed polyhedron. For instance ambo applied twice becomes the same as the expand operation: aa=e, while a truncation after ambo produces bevel: ta=b. There has been no general theory describing what polyhedra can be generated in by any set of operators. Instead all results have been discovered empirically.
Operations on polyhedra
editElements are given from the seed (v,e,f) to the new forms, assuming seed is a convex polyhedron: (a topological sphere, Euler characteristic = 2) An example image is given for each operation, based on a cubic seed. The basic operations are sufficient to generate the reflective uniform polyhedra and their duals. Some basic operations can be made as composites of others. One way to classify operations is by the ratio of the number of edges after the operation to the number before: for a large class of operations, this is an integer value that does not vary depending on the seed.[1]
Special forms
- The kis operator has a variation, kn, which only adds pyramids to n-sided faces.
- The truncate operator has a variation, tn, which only truncates order-n vertices.
The operators are applied like functions from right to left. For example, a cuboctahedron is an ambo cube, i.e. t(C) = aC, and a truncated cuboctahedron is t(a(C)) = t(aC) = taC.
Chirality operator
- r – "reflect" – makes the mirror image of the seed; it has no effect unless the seed was made with s or g. Alternately an overline can be used for picking the other chiral form, like s = rs.
The operations are visualized here on cube seed examples, drawn on the surface of the cube, with blue faces that cross original edges, and pink faces that center at original vertices.
| Operator | Example | Name | Alternate construction |
vertices | edges | faces | Description |
|---|---|---|---|---|---|---|---|
| Seed | rr dd |
v | e | f | Seed form | ||
| r | reflect | v | e | f | Mirror image for chiral forms | ||
| d | dual | f | e | v | dual of the seed polyhedron - each vertex creates a new face | ||
| a | ambo | dj djd |
e | 2e | f+v | New vertices are added mid-edges, while old vertices are removed. Also called rectification, or the medial graph in graph theory This creates valence 4 vertices. | |
| j | join | da dad |
v+f | 2e | e | The seed is augmented with pyramids at a height high enough so that 2 coplanar triangles from 2 different pyramids share an edge. This creates quadrilateral faces. | |
| k kn |
kis | nd = dz dtd |
v+f | 3e | 2e | raises a pyramid on each face. Akisation. Also called Kleetope, cumulation,[2] accretion, or pyramid-augmentation. | |
| t tn |
truncate | dn = zd dkd |
2e | 3e | v+f | truncate all vertices. conjugate kis | |
| n | needle | kd = dt dzd |
v+f | 3e | 2e | Dual of truncation, triangulate with 2 triangles across every edge. This bisect faces across all vertices and edges, while removing original edges. This transforms geodesic polyhedron (a,b) into (a+2b,a-b), for a>b. It transforms (a,0) into (a,a), and (a,a) into '(3a,0), and (2,1) into (4,1), etc. | |
| z | zip | dk = td dnd |
2e | 3e | v+f | Dual of kis or truncation of the dual. This create new edges perpendicular to original edges, a truncation beyond "ambo" with new edges "zipped" between original faces. It is also called bitruncation. This transforms Goldberg polyhedron G(a,b) into G(a+2b,a-b), for a>b. It transforms Goldberg G(a,0) into G(a,a), and G(a,a) into G(3a,0), and G(2,1) into G(4,1), etc. | |
| e | expand | aa dod = do |
2e | 4e | v+e+f | Each vertex creates a new face and each edge creates a new quadrilateral. (cantellate) | |
| o | ortho | daa ded = de |
v+e+f | 4e | 2e | Each n-gon faces are divided into n quadrilaterals. | |
| g rg=g |
gyro | dsd = ds | v+2e+f | 5e | 2e | Each n-gon face is divided into n pentagons. | |
| s rs=s |
snub | dgd = dg | 2e | 5e | v+2e+f | "expand and twist" – each vertex creates a new face and each edge creates two new triangles | |
| b | bevel | dkda = ta dmd = dm |
4e | 6e | v+e+f | New faces are added in place of edges and vertices. (cantitruncation) | |
| m | meta medial |
kda = kj dbd = db |
v+e+f | 6e | 4e | Triangulate with added vertices on edge and face centers. |
Generating regular seeds
editAll of the five regular polyhedra can be generated from prismatic generators with zero to two operators:
- Triangular pyramid: Y3 (A tetrahedron is a special pyramid)
- Triangular antiprism: A3 (An octahedron is a special antiprism)
- O = A3
- C = dA3
- Square prism: P4 (A cube is a special prism)
- C = P4
- Pentagonal antiprism: A5
- I = k5A5 (A special gyroelongated dipyramid)
- D = t5dA5 (A special truncated trapezohedron)
The regular Euclidean tilings can also be used as seeds:
- Q = Quadrille = Square tiling
- H = Hextille = Hexagonal tiling = dΔ
- Δ = Deltille = Triangular tiling = dH
Examples
editThe cube can generate all the convex uniform polyhedra with octahedral symmetry. The first row generates the Archimedean solids and the second row the Catalan solids, the second row forms being duals of the first. Comparing each new polyhedron with the cube, each operation can be visually understood.
| Cube "seed" |
ambo | truncate | zip | expand | bevel | snub |
|---|---|---|---|---|---|---|
| C dO |
aC aO |
tC zO |
zC = dkC tO |
aaC = eC eO |
bC = taC taO |
sC sO |
| dual | join | needle | kis | ortho | medial | gyro |
| dC O |
jC jO |
dtC = kdC kO |
kC dtO |
oC oO |
dtaC = mC mO |
gC gO |
The truncated icosahedron, tI or zD, which is Goldberg polyhedron G(2,0), creates more polyhedra which are neither vertex nor face-transitive.
| "seed" | ambo | truncate | zip | expand | bevel | snub |
|---|---|---|---|---|---|---|
| zD tI |
azI atI |
tzD ttI |
tdzD tdtI |
aazD = ezD aatI = etI |
bzD btI |
szD stI |
| dual | join | needle | kis | ortho | medial | gyro |
| dzD dtI |
jzD jtI |
kdzD kdtI |
kzD ktI |
ozD otI |
mzD mtI |
gzD gtI |
Geometric coordinates of derived forms
editIn general the seed polyhedron can be considered a tiling of a surface since the operators represent topological operations so the exact geometric positions of the vertices of the derived forms are not defined in general. A convex regular polyhedron seed can be considered a tiling on a sphere, and so the derived polyhedron can equally be assumed to be positioned on the surface of a sphere. Similar a regular tiling on a plane, such as a hexagonal tiling can be a seed tiling for derived tilings. Nonconvex polyhedra can become seeds if a related topological surface is defined to constrain the positions of the vertices. For example, toroidal polyhedra can derive other polyhedra with point on the same torus surface.
| D |
tD |
aD |
zD = dkD |
eD |
bD = taD |
sD |
| dD |
nD = dtD |
jD = daD |
kD = dtdD |
oD = deD |
mD = dtaD |
gD |
| H |
tH |
aH |
tdH = H |
eH |
bH = taH |
sH |
| dH |
nH = dtH |
jH = daH |
dtdH = kH |
oH = deH |
mH = dtaH |
gH = dsH |
Derived operations
editMixing two or more basic operations leads to a wide variety of forms. There are many more derived operations, for example, mixing two ambo, kis, or expand, along with up to 3 interspaced duals. Using alternative operators like join, truncate, ortho, bevel and medial can simply the names and remove the dual operators. The numbers of total edges of a derived operation can be computed as the product of the number of total edges of each individual operator.
| Operator(s) | d | a j |
k, t n, z |
e o |
g s |
a&k | a&e | k&k | k&e k&a2 |
e&e |
|---|---|---|---|---|---|---|---|---|---|---|
| edge-multiplier | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 9 | 12 | 16 |
| Unique derived operators | 8 | 2 | 8 | 10 | 2 | |||||
The operations are visualized here on cube seed examples, drawn on the surface of the cube, with blue faces that cross original edges, and pink faces that cross original vertices.
| Derived operations | |||||||
|---|---|---|---|---|---|---|---|
| Operator | Example | Name | Alternate construction |
vertices | edges | faces | Description |
| Seed | v | e | f | Seed form | |||
| at | akd |
3e | 6e | v+2e+f | ambo of truncate | ||
| jk | dak | v+2e+f | 6e | 3e | join of kis. Similar to ortho except new quad faces are inserted in place of the original edges | ||
| ak | dajd | 3e | 6e | v+2e+f | ambo of kis. Similar to expand, except new vertices are added on the original edges, forming two triangles. | ||
| jt | dakd = dat | v+2e+f | 6e | 3e | join of truncate. dual of ambo of truncate | ||
| tj | dka | 4e | 6e | v+e+f | truncate join | ||
| ka | v+e+f | 6e | 4e | kis ambo | |||
| ea or ae | aaa | 4e | 8e | v+3e+f | expanded ambo, triple ambo | ||
| oa or je | daaa = jjj | v+3e+f | 8e | 4e | ortho of ambo, triple join | ||
| kt | kdkd dtkd nn |
v+e+f | 9e | 7e | kis truncate, triangulate, dividing edges into 3, and adding new vertices in the center of original faces. It transforms geodesic polyhedron (a,b) into (3a,3b). | ||
| tk | dkdk dktd zz |
v+e+f | 9e | 7e | truncate kis, expand with hexagons around each edge It transforms Goldberg polyhedron G(a,b) into G(3a,3b). | ||
| nk | kdk = dtk = ktd | 7e | 9e | v+e+f | needled kis | ||
| tn | dkdkd = dkt = tkd | 7e | 9e | v+e+f | truncate needle | ||
| tt | dkkd | 7e | 9e | v+e+f | double-truncate | ||
| kk | dttd | v+2e+f | 9e | 6e | double-kis | ||
| nt | kkd = dtt | v+e+f | 9e | 7e | needle truncate | ||
| tz | dkk = ttd | 6e | 9e | v+2e+f | truncate zip | ||
| ke | kaa | v+3e+f | 12e | 8e | Kis expand | ||
| to | dkaa | 8e | 12e | v+3e+f | truncate ortho | ||
| ek | aak | 6e | 12e | v+5e+f | expand kis | ||
| ok | daak = dek | v+5e+f | 12e | 6e | ortho kis | ||
| et | aadkd | 6e | 12e | v+5e+f | expanded truncate | ||
| ot | daadkd = det | v+5e+f | 12e | 6e | ortho truncate | ||
| te or ba | dkdaa | 8e | 12e | v+3e+f | truncate expand | ||
| ko or ma | kdaa = dte ma = mj |
v+3e+f | 12e | 8e | kis ortho | ||
| ab or am | aka = ata | 6e | 12e | v+5e+f | ambo bevel | ||
| jb or jm | daka = data | v+5e+f | 12e | 6e | joined bevel | ||
| ee | aaaa | v+7e+f | 16e | 8e | double-expand | ||
| oo | daaaa = dee | 8e | 16e | v+7e+f | double-ortho | ||
Chiral derived operations
editThere are more derived operators mixing at least one gyro with ambo, kis or expand, and up to 3 duals.
| Operator(s) | d | a | k | e | g | a&g | k&g | e&g | g&g |
|---|---|---|---|---|---|---|---|---|---|
| edge-multiplier | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 | 25 |
| Unique derived operators | 4 | 8 | 4 | 2 | |||||
Extended operators
editThese extended operators can't be created in general from the basic operations above. Some can be created in special cases with k and t operators only applied to specific sided faces and vertices. For example, a chamfered cube, cC, can be constructed as t4daC, as a rhombic dodecahedron, daC or jC, with its valence-4 vertices truncated. A lofted cube, lC is the same as t4kC. And a quinto-dodecahedron, qD can be constructed as t5daaD or t5deD or t5oD, a deltoidal hexecontahedron, deD or oD, with its valence-5 vertices truncated.
Some further extended operators suggest a sequence and are given a following integer for higher order forms. For example, ortho divides a square face into 4 squares, and a o3 can divide into 9 squares. o3 is a unique construction while o4 can be derived as oo, ortho applied twice. The loft operator can include an index, similar to kis, to limit the effect to faces with that number of sides.
The chamfer operation creates Goldberg polyhedra G(2,0), with new hexagons between original faces. Sequential chamfers create G(2n,0).
| Extended operations | |||||||
|---|---|---|---|---|---|---|---|
| Operator | Example | Name | Alternate construction |
vertices | edges | faces | Description |
| Seed | v | e | f | Seed form | |||
| c | chamfer | dud | v + 2e | 4e | f + e | An edge-truncation. New hexagonal faces are added in place of edges. Goldberg (0,2) | |
| - | - | dc | f + e | 4e | v + 2e | Dual of chamfer | |
| u | subdivide | dcd | v+e | 4e | f+2e | Ambo while retaining original vertices Similar to Loop subdivision surface for triangle faces | |
| - | cd | f+2e | 4e | v+e | dual to subdivision | ||
| l ln |
loft | v+2e | 5e | f+2e | An augmentation of each face by prism, adding a smaller copy of each face with trapezoids between the inner and outer ones. | ||
| dl dln |
f+2e | 5e | v+2e | Dual to loft | |||
| ld lnd |
f+2e | 5e | v+2e | loft of dual | |||
| dld dlnd |
v+2e | 5e | f+2e | Conjugate to loft | |||
| dL0 | f+3e | 6e | v+2e | Dual to joined-lace | |||
| L0d | f+2e | 6e | v+3e | Joined-lace of dual | |||
| dL0d | v+3e | 6e | f+2e | Conjugate joined-lace | |||
| q | quinto | v+3e | 6e | f+2e | ortho followed by truncation of vertices centered on original faces. This create 2 new pentagons for every original edge. | ||
| - | dq | f+2e | 6e | v+3e | dual of quinto | ||
| qd | v+2e | 6e | f+3e | quinto of dual | |||
| - | dqd | f+3e | 6e | v+2e | conjugate of quinto | ||
| L0 | joined-lace | v+2e | 6e | f+3e | Similar to lace, except new with quad faces across original edges | ||
| L Ln |
Lace | v+2e | 7e | f+4e | An augmentation of each face by an antiprism, adding a twist smaller copy of each face, and triangles between. An index can be added to limit the operation to faces of that many sides. | ||
| dL dLn |
f+4e | 7e | v+2e | Dual of laced | |||
| Ld Ldn |
f+2e | 7e | v+4e | Lace of dual | |||
| dLd dLnd |
v+4e | 7e | f+2e | Dual of lace of dual | |||
| K Kn |
staKe | v+2e+f | 7e | 4e | Subdivide faces with central quads, and triangles. An index can be added to limit the operation to faces of that many sides. | ||
| dK dKn |
4e | 7e | v+2e+f | Dual of stake | |||
| Kd | v+2e+f | 7e | 4e | Stake of dual | |||
| dKd | 4e | 7e | v+2e+f | Conjugate of stake | |||
| M3 | edge-medial-3 | v+2e+f | 7e | 4e | Similar to m3 except no diagonal edges added, creating quad faces there | ||
| dM3 | 4e | 7e | v+2e+f | dual of edge-medial-3 | |||
| M3d | v+2e+f | 7e | 4e | edge-medial-3 of dual | |||
| dM3d | 4e | 7e | v+2e+f | Conjugate of edge-medial-3 | |||
| M0 | joined-medial | v+2e+f | 8e | 5e | Like medial, but new rhombic faces in place of original edges. | ||
| dM0 | v+2e+f | 8e | 5e | dual of joined-medial | |||
| M0d | v+2e+f | 8e | 5e | joined-medial of dual | |||
| dM0d | 5e | 8e | v+2e+f | Conjugate of joined-medial | |||
| m3 | medial-3 | v+2e+f | 9e | 7e | triangulate with 2 vertices added on edge and face centers. | ||
| b3 | bevel-3 | dm3 | 7e | 9e | v+2e+f | dual to medial-3 | |
| m3d | 7e | 9e | v+2e+f | medial-3 of dual | |||
| dm3d | v+2e+f | 9e | 7e | conjugate of medial-3 | |||
| o3 | ortho-3 | de3 | v+4e | 9e | f+4e | ortho operator with 3 edge divisions | |
| e3 | expand-3 | do3 | f+4e | 9e | v+4e | expand operator with 3 edge divisions | |
| X | cross | v+f+3e | 10e | 6e | Combination of kis and subdivide operation. Original edges are divided in half, with triangle and quad faces. | ||
| dX | 6e | 10e | v+f+3e | Dual to cross | |||
| Xd | 6e | 10e | v+f+3e | Cross of dual | |||
| dXd | v+f+3e | 10e | 6e | Conjugate of cross | |||
| m4 | medial-4 | v+3e+f | 12e | 8e | triangulate with 3 vertices added on edge and face centers. | ||
| u5 | subdivide-5 | v+8e | 25e | f+16e | Subdivide edges into 5th This operator divides edges and faces so there are 6 triangles around each new vertex. | ||
Extended chiral operators
editThese operators can't be created in general from the basic operations above. Geometric artist George W. Hart created an operation he called a propellor.
- p – "propellor" (A rotation operator that creates quadrilaterals at the vertices). This operation is self-dual: dpX=pdX.
| Chiral extended operations | |||||||
|---|---|---|---|---|---|---|---|
| Operator | Example | Name | Alternate construction |
vertices | edges | faces | Description |
| "Seed" | v | e | f | Seed form | |||
| p rp=p |
propellor | v + 2e | 5e | f + 2e | A gyro followed by an ambo of vertices centered at original faces | ||
| - | - | dp = pd | f + 2e | 5e | v + 2e | Same vertices as gyro, except new faces at original vertices | |
| - | 4e | 7e | v+2e+f | Like snub, except pentagons are around original faces rather than triangles | |||
| - | - | - | v+2e+f | 7e | 4e | ||
| w=w2=w2,1 rw=w |
whirl | v+4e | 7e | f+2e | gyro followed by truncation of vertices centered at original faces. This create 2 new hexagons for every original edge, Goldberg (2,1) The derived operator wrw transforms G(a,b) into G(7a,7b). | ||
| v rv=v |
volute | dwd | f+2e | 7e | v+4e | dual of whirl, a snub followed by kis on original faces. The derived operator vrv transforms geodesic (a,b) into (7a,7b). | |
| g3 rg3=g3 |
gyro-3 | v+6e | 11e | f+4e | Gyro operation create 3 pentagons along each original edge | ||
| s3 rs3=s3 |
snub-3 | dg3d = dg3 | f+4e | 11e | v+6e | Dual of gyro-3, snub operation which divides edges into 4 middle triangles with triangles at the original vertices | |
| w3,1 rw3,1=w3,1 |
whirl-3,1 | v+8e | 13e | f+4e | create 4 new hexagons for every original edge, Goldberg (3,1) | ||
| w3=w3,2 rw3=w3 |
whirl-3,2 | v+12e | 19e | f+6e | create 12 new hexagons for every original edge, Goldberg (3,2) | ||
Operations that preserve original edges
editThese augmentation operations retain original edges, and allowing the operator to apply to any independent subset of faces. Conway notation supports an optional index to these operators to specific how many sides affected faces will have.
| Operator | kis | loft | lace | stake | kis-kis |
|---|---|---|---|---|---|
| Example | kC | lC | LC | KC | kkC |
| Edges | 3e | 5e | 6e | 7e | 9e |
| Image on cube |
|||||
| Augmentation | Pyramid | Prism | Antiprism |
Subdivision
editA subdivision operation divides original edges into n new edges and face interiors into smaller triangles or other polygons.
Square subdivision
editThe ortho operator can be applied in series for powers of two quad divisions. Other divisions can be produced by the product of factorized divisions. The propellor operator applied in sequence, in reverse chiral directions produces a 5-ortho division. If the seed polyhedron has nonquadrilaeral faces, they will be retained as smaller copies for odd-ortho operators.
Chiral hexagonal subdivision
editA whirl operation creates Goldberg polyhedra, G(2,1) with new hexagonal faces around each original vertex. Two sequential whirls create G(3,5). In general, a whirl can transform a G(a,b) into G(a + 3b,2a − b) for a>b and the same chiral direction. If chiral directions are reversed, G(a,b) becomes G(2a + 3b,a − 2b) if a ≥ 2b, and G(3a + b,2b − a) if a < 2b. Higher n-whirls can be defined as G(n,n − 1), and m,n-whirl G(m,n).
Whirl-n operators generate Goldberg polyhedra (n,n − 1) and can be defined by dividing a seed polyhedron's edges into 2n − 1 subedges as rings around brick pattern hexagons. Some can also be generated by composite operators with smaller Whirl-m,n operators.
The product of whirl-n and its reverse generates a (3n2 − 3n + 1,0) Goldberg polyhedron. wrw generates (7,0) w3rw3 generates (19,0), w4rw4 generates (37,0), w5rw5 generates (61,0), and w6rw6 generates (91,0). The product of two whirl-n is ((n − 1)(3n − 1),2n − 1) or (3n2 − 4n + 1,2n − 1). The product of wa by wb gives (3ab − 2(a + b) + 1,a + b − 1), and wa by reverse wb is (3ab − a − 2b + 1,a − b) for a ≥ b.
The product of two identical whirl-n operators generates Goldberg ((n − 1)(3n − 1),2n − 1). The product of a k-whirl and zip is (3k − 2,1).
| Whirl-n operators | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Seed | Whirl | Whirl-3 | Whirl-4 | Whirl-5 | Whirl-6 | Whirl-7 | Whirl-8 | Whirl-9 | Whirl-10 | Whirl-11 | Whirl-12 | Whirl-13 | Whirl-14 | Whirl-15 | Whirl-16 | Whirl-17 | Whirl-18 | Whirl-19 | Whirl-20 | Whirl-n |
| Operator (Composite) |
– | w=w2 | w3 | w4 | w5 | w6 wrw3,1 |
w7 | w8 w3,1w3,1 |
w9 ww5,1 |
w10 | w11 | w12 | w13 ww7,2 |
w14 | w15 | w16 ww9,2 |
w17 w3w6,1 |
w18 | w19 w3,1w7,3 |
w20 ww11,3 |
wn |
| Goldberg | (1,0) | (2,1) | (3,2) | (4,3) | (5,4) | (6,5) | (7,6) | (8,7) | (9,8) | (10,9) | (11,10) | (12,11) | (13,12) | (14,13) | (15,14) | (16,15) | (17,16) | (18,17) | (19,18) | (20,19) | (n,n − 1) |
| T composite |
1 | 7 | 19 | 37 | 61 | 91 7×13 |
127 | 169 13×13 |
217 7×31 |
271 | 331 | 397 | 469 7×67 |
547 | 631 | 721 7×103 |
817 19×43 |
919 | 1027 13×79 |
1141 7×163 |
3n(n − 1) + 1 |
| Example | |||||||||||||||||||||
| Vertices | v | v + 4e | v + 12e | v + 24e | v + 40e | v + 60e | v + 84e | v + 112e | v + 144e | v + 180e | v + 220e | v + 264e | v + 312e | v + 364e | v + 420e | v + 480e | v + 544e | v + 612e | v + 684e | v + 760e | v + 2n(n − 1)e |
| Edges | e | 7e | 19e | 37e | 61e | 91e | 127e | 169e | 217e | 271e | 331e | 397e | 469e | 547e | 631e | 721e | 817e | 919e | 1027e | 1141e | e + 3n(n − 1)e |
| Faces | f | f + 2e | f + 6e | f + 12e | f + 20e | f + 30e | f + 42e | f + 56e | f + 72e | f + 90e | f + 110e | f + 132e | f + 156e | f + 182e | f + 210e | f + 240e | f + 272e | f + 306e | f + 342e | f + 380e | f + n(n − 1)e |
| wnwn | (1,0) | (5,3) | (16,5) | (33,7) | (56,9) | (85,11) | (120,13) | (161,15) | (208,17) | (261,19) | (320,21) | (385,23) | (456,25) | (533,27) | (616,29) | (705,31) | (800,33) | (901,35) | (1008,37) | (1121,39) | ((n – 1)(3n − 1),2n − 1) |
| wnrwn | (1,0) | (7,0) | (19,0) | (37,0) | (61,0) | (91,0) | (127,0) | (169,0) | (217,0) | (271,0) | (331,0) | (397,0) | (469,0) | (547,0) | (631,0) | (721,0) | (817,0) | (919,0) | (1027,0) | (1141,0) | (1+3n(n − 1),0) |
| wnz | (1,1) | (4,1) | (7,1) | (10,1) | (13,1) | (16,1) | (19,1) | (22,1) | (25,1) | (28,1) | (31,1) | (34,1) | (37,1) | (40,1) | (43,1) | (46,1) | (49,1) | (52,1) | (55,1) | (58,1) | (3n − 2,1) |
Triangulated subdivision
editAn operation un divides faces into triangles with n-divisions along each edge, called an n-frequency subdivision in Buckminster Fuller's geodesic polyhedra.[3]
Conway polyhedron operators can construct many of these subdivisions.
If the original faces are all triangles, the new polyhedra will also have all triangular faces, and create triangular tilings within each original face. If the original polyhedra has higher polygons, all new faces won't necessarily be triangles. In such cases a polyhedron can first be kised, with new vertices inserted in the center of each face.
| Subdivisions on a cube example | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Operator | u1 | u2 = u |
u3 = nn |
u4 = uu |
u5 | u6 = unn |
u7 =vrv |
u8 = u3 |
u9 =n4 |
| Example | |||||||||
| Conway | C | uC | nnC | uuC | u5C | unnC | vrvC | u3C | n4C |
| Vertices | v | v+e | v+e+f | v+4e | v+8e | v+11e+f | v+16e | v+21e | v+26e+f |
| Edges | e | 4e | 9e | 16e | 25e | 36e | 49e | 64e | 81e |
| Faces | f | f+2e | 7e | f+8e | f+16e | 24e | f+32e | f+42e | 54e |
| Full triangulation | |||||||||
| Operator | u1k | u2k =uk |
u3k =nnk |
u4k =uuk |
u5k | u6k =unnk |
u7k =vrvk |
u8k =u3k |
u9k =n4k |
| Example | |||||||||
| Conway | kC | ukC | nnkC | uukC | u5kC | unnkC | vrvkC | u3kC | n4kC |
| Goldberg dual | {3,n+}1,1 | {3,n+}2,2 | {3,n+}3,3 | {3,n+}4,4 | {3,n+}5,5 | {3,n+}6,6 | {3,n+}7,7 | {3,n+}8,8 | {3,n+}9,9 |
Geodesic polyhedra
editConway operations can duplicate some of the Goldberg polyhedra and geodesic duals. The number of vertices, edges, and faces of Goldberg polyhedron G(m,n) can be computed from m and n, with T = m2 + mn + n2 = (m + n)2 − mn as the number of new triangles in each subdivided triangle. (m,0) and (m,m) constructions are listed below from Conway operators.
Class I
editFor Goldberg duals, an operator uk is defined here as dividing faces with k edge subdivisions, with Conway u = u2, while its conjugate operator, dud is chamfer, c. This operator is used in computer graphics, loop subdivision surface, as recursive iterations of u2, doubling each application. The operator u3 is given a Conway operator nn=kt, and its conjugate operator zz=tk. The product of two whirl operators with reverse chirality, wrw or ww, produces 7 subdivisions as Goldberg polyhedron G(7,0), thus u7=vrv. Higher subdivision and whirl operations in chiral pairs can construct more class I forms. w(3,1)rw(3,1) gives Goldberg G(13,0). w(3,2)rw(3,2) gives G(19,0).
| Class I: Subdivision operations on an icosahedron as geodesic polyhedra | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (m,0) | (1,0) | (2,0) | (3,0) | (4,0) | (5,0) | (6,0) | (7,0) | (8,0) | (9,0) | (10,0) | (11,0) | (12,0) | (13,0) | (14,0) | (15,0) | (16,0) |
| T | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | 256 |
| Operation Composite |
u1 | u2=u =dcd |
u3=nn =kt |
u4 =u22 =dccd |
u5 | u6=u2u3 =dctkd |
u7 =vv =dwrwd |
u8=u23 =dcccd |
u9=u32 =ktkt |
u10=u2u5 | u11 | u12=u22u3 =dccdkt |
u13 v3,1v3,1 |
u14=u2u7 =uvv =dcwrwd |
u15= u3u5 =u5nn |
u16=u24 =dccccd |
| Face triangle |
||||||||||||||||
| Icosahedron Conway Geodesic |
I {3,5+}1,0 |
uI=k5aI {3,5+}2,0 |
nnI=ktI {3,5+}3,0 |
u2I {3,5+}4,0 |
{3,5+}5,0 |
unnI {3,5+}6,0 |
vrvI {3,5+}7,0 |
u3I {3,5+}8,0 |
nn2I {3,5+}9,0 |
{3,5+}10,0 |
{3,5+}11,0 |
u2nnI {3,5+}12,0 |
{3,5+}13,0 |
uvrvI {3,5+}14,0 |
{3,5+}15,0 |
u4I {3,5+}16,0 |
| Dual operator | c | zz =tk |
cc | c5 | czz =ctk |
ww =wrw |
ccc | z2 =tktk |
cc5 | c11 | cczz =cctk |
w3,1w3,1 | cww =cwrw |
c5zz | cccc | |
| Dodecahedron Conway Goldberg |
D {5+,3}1,0 |
cD {5+,3}2,0 |
zzD {5+,3}3,0 |
ccD {5+,3}4,0 |
c3D {5+,3}5,0 |
czzD {5+,3}6,0 |
wrwD {5+,3}7,0 |
cccD {5+,3}8,0 |
zz2D {5+,3}9,0 |
cc5D {5+,3}10,0 |
c11D {5+,3}11,0 |
cczzD {5+,3}12,0 |
w3,1rw3,1D {5+,3}13,0 |
cwrwD {5+,3}14,0 |
c5zzD {5+,3}15,0 |
ccccD G{5+,3}16,0 |
Class II
editOrthogonal subdivision can also be defined, using operator n=kd. The operator transforms geodesic polyhedron (a,b) into (a+2b,a-b), for a>b. It transforms (a,0) into (a,a), and (a,a) into (3a,0). The operator z=dk does the same for the Goldberg polyhedra.
This is also called a Triacon method, dividing into subtriangles along their height, so they require an even number of triangles along each edge.
| Class II: Orthogonal subdivision operations | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (m,m) | (1,1) | (2,2) | (3,3) | (4,4) | (5,5) | (6,6) | (7,7) | (8,8) | (9,9) | (10,10) | (11,11) | (12,12) | (13,13) | (14,14) | (15,15) | (16,16) |
| T= m2×3 |
3 1×3 |
12 4×3 |
27 3×3 |
48 24×3 |
75 25×3 |
108 36×3 |
147 49×3 |
192 64×3 |
243 81×3 |
300 100×3 |
363 121×3 |
432 144×3 |
507 169×3 |
588 196×3 |
675 225×3 |
768 256×3 |
| Operation | u1n n =kd |
u2n =un =dct |
u3n =n3 =ktkd |
u4n =u22n =dcct |
u5n | u6n =u2=u3n =dctkt |
u7n =vvn =dwrwt |
u8n =u23n =dccct |
u9n =u32n =ktktkd |
u10n =u2u5n |
u11n | u12n =u22u3n =dcctkt |
u13n | u14n =u2u7n =dcwrwt |
u15n =u3u5n |
u16n =u24n =dcccct |
| Face triangle |
||||||||||||||||
| Icosahedron Conway Geodesic |
nI {3,5+}1,1 |
unI {3,5+}2,2 |
nnnI {3,5+}3,3 |
u2nI {3,5+}4,4 |
{3,5+}5,5 |
unnnI {3,5+}6,6 |
vrvnI {3,5+}7,7 |
u3nI {3,5+}8,8 |
n5I {3,5+}9,9 |
{3,5+}10,10 |
{3,5+}11,11 |
u2n3I {3,5+}12,12 |
{3,5+}13,13 |
dcwrwdnI {3,5+}14,14 |
{3,5+}15,15 |
u4nI {3,5+}16,16 |
| Dual operator | z =dk |
cz =cdk |
z3 =tkdk |
c2z =ccdk |
c5z | cz3 =ctkdk |
wwz =wrwdk |
c3z =cccdk |
z5 =tktkdk |
cc5z | c11z | c2z3 =c2tkdk |
c13z | cwwz =cwrwdk |
c3c5z | c4z =ccccdk |
| Dodecahedron Conway Goldberg |
zD {5+,3}1,1 |
czD {5+,3}2,2 |
zzzD {5+,3}3,3 |
cczD {5+,3}4,4 |
{5+,3}5,5 |
czzzD {5+,3}6,6 |
wrwzD {5+,3}7,7 |
c3zD {5+,3}8,8 |
z5D {5+,3}9,9 |
{5+,3}10,10 |
G{5+,3}11,11 |
cczzzD {5+,3}12,12 |
{5+,3}13,13 |
cwrwzD G{5+,3}14,14 |
{5+,3}15,15 |
cccczD {5+,3}16,16 |
Class III
editMost geodesic polyhedra and dual Goldberg polyhedra G(n,m) can't be constructed from derived Conway operators. The whirl operation creates Goldberg polyhedra, G(2,1) with new hexagonal faces around each original vertex, and n-whirl genereates G(n,n-1). On icosahedral symmetry forms, t5g is equivalent to whirl in this case. The v=volute operation represents the triangular subdivision dual of whirl. On icosahedral forms it can be made by the derived operator k5s, a pentakis snub.
Two sequential whirls create G(3,5). In general, a whirl can transform a G(a,b) into G(a+3b,2a-b) for a>b and the same chiral direction. If chiral directions are reversed, G(a,b) becomes G(2a+3b,a-2b) if a>=2b, and G(3a+b,2b-a) if a<2b.
| Class III: Unequal subdivision operations | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Operation Composite |
v2,1 =v |
v3,1 | v3,2=v3 | v4,1 =vn |
v4,2 =vu |
v5,1 | v4,3=v4 | v5,2 =v3n |
v6,1 | v6,2 =v3,1u |
v5,3 =vv |
v7,1 =v3n |
v5,4=v5 | v6,3 =vnn |
v7,2 | |
| T | 7 | 13 | 19 | 21 7×3 |
28 7×4 |
31 | 37 | 39 13×3 |
43 | 52 13×4 |
49 7×7 |
57 19×3 |
61 | 63 9×7 |
67 | |
| Face triangle |
||||||||||||||||
| Icosahedron Conway Geodesic |
vI {3,5+}2,1 |
v3,1I {3,5+}3,1 |
v3I {3,5+}3,2 |
vnI {3,5+}4,1 |
vuI {3,5+}4,2 |
{3,5+}5,1 |
v4I {3,5+}4,3 |
v3nI {3,5+}5,2 |
{3,5+}6,1 |
v3,1uI {3,5+}6,2 |
vvI {3,5+}5,3 |
v3nI {3,5+}7,1 |
v5I {3,5+}5,4 |
vnnI {3,5+}6,3 |
v7,2I {3,5+}7,2 | |
| Operator | w | w3,1 | w3 | wz | wc | w5,1 | w4 | w3,1z | w6,1 | w3,1c | ww | w3z | w5 | wzz | w7,2 | |
| Dodecahedron Conway |
wD {5+,3}2,1 |
w3,1D {5+,3}3,1 |
w3D {5+,3}3,2 |
wzD {5+,3}4,1 |
wcD {5+,3}4,2 |
w5,1D {5+,3}5,1 |
w4D {5+,3}4,3 |
w3zD {5+,3}5,2 |
{5+,3}6,1 |
w3,1cD {5+,3}6,2 |
wwD {5+,3}5,3 |
w3zD {5+,3}7,1 |
w5D {5+,3}5,4 |
wzzD {5+,3}6,3 |
w7,2D {5+,3}7,2 | |
| More class III: Unequal subdivision operations | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Operation Composite |
v8,1 | v6,4 =v3u |
v7,3 | v8,2 =wcz |
v6,5=v6 =vrv3,1 |
v9,1 =vv3,1 |
v7,4 | v8,3 | v9,2 | v7,5 | v10,1 =v4n |
v8,4 =vuu |
v9,3 =v3,1nn |
v7,6=v7 | v8,6 v4u | ||||
| T | 73 | 76 19×4 |
79 | 84 7×4×3 |
91 13×7 |
93 | 97 | 103 | 109 | 111 37×3 |
112 7×4×4 |
117 13×9 |
127 | 148 37×4 | |||||
| Face triangle |
|||||||||||||||||||
| Icosahedron Conway Geodesic |
v8,1I {3,5+}8,1 |
v3uI {3,5+}6,4 |
v7,3I {3,5+}7,3 |
vunI {3,5+}8,2 |
vv3,1I {3,5+}6,5 |
vrv3,1I {3,5+}9,1 |
v7,4I {3,5+}7,4 |
v8,3I {3,5+}8,3 |
v9,2I {3,5+}9,2 |
v7,5I {3,5+}7,5 |
v4nI {3,5+}10,1 |
vuuI {3,5+}8,4 |
v3,1nnI {3,5+}9,3 |
v7I {3,5+}7,6 |
v4uI {3,5+}8,6 | ||||
| Operator | w8,1 | wrw3,1 | w7,3 | w3,1c | wcz | w3,1w | w7,4 | w8,3 | w9,2 | w7,5 | w4z | wcc | w3,1zz | w7 | w4c | ||||
| Dodecahedron Conway |
w8,1D {5+,3}8,1 |
w3cD {5+,3}6,4 |
w7,3D {5+,3}7,3 |
wczD {5+,3}8,2 |
ww3,1D {5+,3}6,5 |
wrw3,1D {5+,3}9,1 |
w7,4D {5+,3}7,4 |
w8,3D {5+,3}8,3 |
w9,2D {5+,3}9,2 |
w7,5D {5+,3}7,5 |
w4zD {5+,3}10,1 |
wccD {5+,3}8,4 |
w3,1nnD {5+,3}9,3 |
w7D {5+,3}7,6 |
w4cD {5+,3}8,6 | ||||
Example polyhedra by symmetry
editIterating operators on simple forms can produce progressively larger polyhedra, maintaining the fundamental symmetry of the seed element.
Tetrahedral symmetry
edit-
tatT
-
stT
-
XT (10e)
-
dXT (10e)
-
m3T
-
b3T
Octahedral symmetry
edit-
daC (2e)
-
cO (4e)
-
dakC (6e)
-
m3C (6e)
-
m3O (6e)
-
b3C (6e)
-
b3O (6e)
-
atC (6e)
-
qC (6e)
-
edaC (8e)
-
dktO=tkC (9e)
-
XO (10e)
-
XC (10e)
-
dXO (10e)
-
dXC (10e)
-
cdkC (12e)
-
ccC (16e)
-
tkdkC (18e)
-
tatO (18e)
-
tatC (18e)
-
l6l8taC (22e)
-
ccdkC (48e)
-
wrwC (49e)
-
cccC (64e)
-
tktkC (81e)
- Chiral
Icosahedral symmetry
edit-
kD = daD (2e)
-
cI (4e) *
-
atD (6e)
-
qD (6e)
-
m3D (6e)
-
m3I (6e)
-
b3D (6e)
-
b3I (6e)
-
edaD (8e) *
-
tkdD (9e) *
-
gaD (10e) *
-
XI (10e)
-
XD (10e)
-
dXI (10e)
-
dXD (10e)
-
cdkD (12e)
-
m3aI (12e)
-
tatI = takD (18e)
-
tatD (18e)
-
atkD (18e)
-
m3tD (18e)
-
qtI = t5t6otI (18e)
-
dqtI = k5k6etI (18e)
-
actI (24e)
-
kdktI (27e)
-
tktI (27e)
-
dctkD (36e)
-
ctkD (36e)
- Chiral
-
dsD (5e)
-
sD (5e)
-
wD (7e)
-
k5sD (7e)
-
saD (10e)
-
saD (10e)
-
g3D (11e)
-
s3D (11e)
-
g3I (11e)
-
s3I (11e)
-
stI (15e)
-
stD (15e)
-
wtI (21e)
-
k5k6stI (21e)
Dihedral symmetry
edit-
t4daA4=cA4
-
t4daA4=cA4 (side)
-
t4daA4=cA4 (top)
-
tA4
-
tA5
-
eP3 = aaP3
-
eA4 = aaA4
Toroidal symmetry
editTorioidal tilings exist on the flat torus on the surface of a duocylinder in four dimensions but can be projected down to three dimensions as an ordinary torus. These tilings are topologically similar subsets of the Euclidean plane tilings.
-
A 1x1 regular square torus, {4,4}1,0
-
A regular 4x4 square torus, {4,4}4,0
-
tQ24×12 projected to torus
-
taQ24×12 projected to torus
-
actQ24×8 projected to torus
-
tH24×12 projected to torus
-
taH24×8 projected to torus
-
kH24×12 projected to torus
Euclidean square symmetry
edit-
tQ
-
cQ
-
akQ
Euclidean triangular symmetry
edit-
tH
-
cΔ
-
cH
-
ctH
-
dakH
-
aaaH
-
aaaH, equilateral
See also
edit- Uniform polyhedra
- Computer graphics algorithms:
- Doo–Sabin subdivision surface – expand operator
- Catmull–Clark subdivision surface – ortho operator
- Goldberg polyhedron
- Goldberg–Coxeter construction
- Symmetrohedron
References
edit- ^ Brinkmann, G.; Goetschalckx, P.; Schein, S. (2017). "Goldberg, Fuller, Caspar, Klug and Coxeter and a general approach to local symmetry-preserving operations". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science. 473 (2206): 20170267. arXiv:1705.02848. doi:10.1098/rspa.2017.0267.
- ^ http://mathworld.wolfram.com/Cumulation.html
- ^ Anthony Pugh, Polyhedra: a visual approach, (1976), Chapter 6, Geodesic polyhedra, p.63 [1]
- George W. Hart, Sculpture based on Propellorized Polyhedra, Proceedings of MOSAIC 2000, Seattle, WA, August, 2000, pp. 61–70 [2]
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
- Chapter 21: Naming the Archimedean and Catalan polyhedra and Tilings
- Visualization of Conway Polyhedron Notation Hidetoshi Nonaka, World Academy of Science, Engineering and Technology 50 2009
External links and references
edit- George Hart's Conway interpreter: generates polyhedra in VRML, taking Conway notation as input. Also includes helpful explanations of the operations.
- Vertex- and edge-truncation of the Platonic and Archimedean solids leading to vertex-transitive polyhedra Livio Zefiro
- polyHédronisme: generates polyhedra in HTML5 canvas, taking Conway notation as input
- Weisstein, Eric W. "Conway Polyhedron Notation". MathWorld.
- John Conway's notation Visualization of Conway Polyhedron Notation
- Weisstein, Eric W. "Truncation". MathWorld. (truncate)
- Weisstein, Eric W. "Rectification". MathWorld. (ambo)
- Weisstein, Eric W. "Cumulation or Apiculation". MathWorld. (kis)
- Conway operators, PolyGloss, Wendy Krieger
- Derived Solids